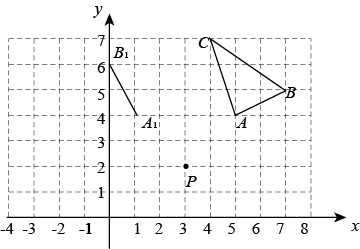
1.
如图,在平面直角坐标系中,点 的坐标为
的坐标为 , 将线段
, 将线段 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 , 再将其长度伸长为
, 再将其长度伸长为 的
的 倍,得到线段
倍,得到线段 ;又将线段
;又将线段 绕
绕 点按顺时针方向旋转
点按顺时针方向旋转 长度伸长为
长度伸长为 的
的 倍,得到线段
倍,得到线段 ;如此下去,得到线段
;如此下去,得到线段 ,
,  ,
,  ,
,  为正整数
为正整数 , 则点
, 则点 的坐标是 .
的坐标是 .

【考点】
坐标与图形变化﹣旋转;
基础巩固
能力提升
变式训练
拓展培优
真题演练