1.
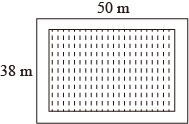
三国时期的数学家赵爽,在其所著的《勾股圆方图注》中记载用图形的方法来解一元二次方程,四个相等的矩形(每一个矩形的面积都是35)拼成如图所示的一个大正方形,利用所给的数据,能得到的方程是( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
一元二次方程的应用-几何问题;
能力提升
变式训练
拓展培优
真题演练