1.
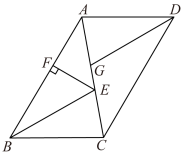
如图,直线 ∥直线
∥直线 ,
,  .
.

(1)
补全对 的说理过程;
(2)
若
的说理过程;
(2)
若 平分
平分 , 且
, 且 , 求
, 求 的度数.
的度数.
∵(已知),
∴
( ).
∵( ),
∴
(等量代换),
∴( );
【考点】
平行线的判定与性质;
角平分线的性质;
能力提升
真题演练