1.
综合与实践:

(1)
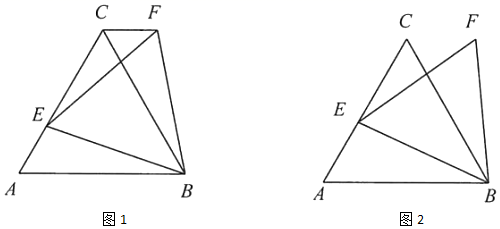
问题探究:图1是古希腊数学家欧几里得所著的《几何原本》中给出的角平分线作图法:在 和
和 上分别取点
上分别取点 和
和 , 使得
, 使得 , 连接
, 连接 , 以
, 以 为边作等边三角形
为边作等边三角形 , 则
, 则 就是
就是 的平分线.请写出
的平分线.请写出 平分
平分 的依据____;
A.
SSS
B.
SAS
C.
ASA
D.
AAS
(2)
类比迁移:小明根据以上信息研究发现:
的依据____;
A.
SSS
B.
SAS
C.
ASA
D.
AAS
(2)
类比迁移:小明根据以上信息研究发现: 不一定必须是等边三角形,只需
不一定必须是等边三角形,只需 即可,他查阅资料:我国古代已经用角尺平分任意角,做法如下:如图2,在
即可,他查阅资料:我国古代已经用角尺平分任意角,做法如下:如图2,在 的边
的边 上分别取
上分别取 , 移动角尺,使角尺两边相同刻度分别与点
, 移动角尺,使角尺两边相同刻度分别与点 重合,则过角尺顶点
重合,则过角尺顶点 的射线
的射线 是
是 的平分线,请证明此做法的合理性;
(3)
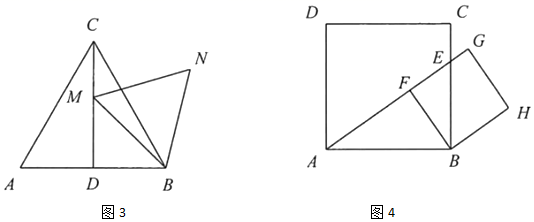
拓展实践:如图3,四边形
的平分线,请证明此做法的合理性;
(3)
拓展实践:如图3,四边形 中,
中, , 对角线
, 对角线 与
与 相交于点
相交于点 , 我们把这种两组邻边分别相等的四边形叫做“筝形”.猜想该“筝形”
, 我们把这种两组邻边分别相等的四边形叫做“筝形”.猜想该“筝形” 的面积
的面积 与对角线
与对角线 的数量关系,并进行证明.
的数量关系,并进行证明.
【考点】
三角形全等的判定;
等边三角形的性质;