1.
在数学兴趣小组活动中,小亮进行数学探究活动.
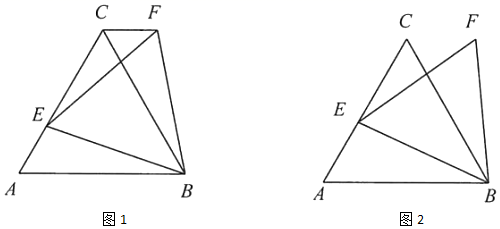
(1)
 是边长为3的等边三角形,E是边
是边长为3的等边三角形,E是边  上的一点,且
上的一点,且  ,小亮以
,小亮以  为边作等边三角形
为边作等边三角形  ,如图1,求
,如图1,求  的长;
(2)
的长;
(2)
 是边长为3的等边三角形,E是边
是边长为3的等边三角形,E是边  上的一个动点,小亮以
上的一个动点,小亮以  为边作等边三角形
为边作等边三角形  ,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
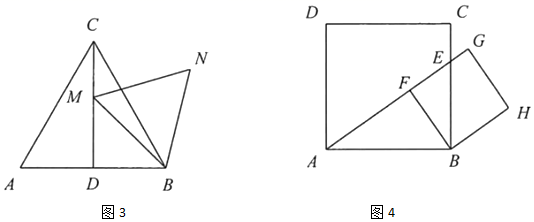
(3)
,如图2,在点E从点C到点A的运动过程中,求点F所经过的路径长;
(3)
 是边长为3的等边三角形,M是高
是边长为3的等边三角形,M是高  上的一个动点,小亮以
上的一个动点,小亮以  为边作等边三角形
为边作等边三角形  ,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)
正方形
,如图3,在点M从点C到点D的运动过程中,求点N所经过的路径长;
(4)
正方形  的边长为3,E是边
的边长为3,E是边  上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形
上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形  ,其中点F、G都在直线
,其中点F、G都在直线  上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为,点G所经过的路径长为.
上,如图4,当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为,点G所经过的路径长为.
【考点】
三角形全等的判定;
等边三角形的性质;
勾股定理;
正方形的性质;
弧长的计算;


