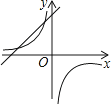
1.
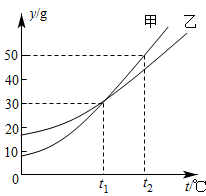
如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程 、
、 与时间
与时间 的关系,观察图象并回答下列问题:
的关系,观察图象并回答下列问题:

(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙有事耽搁,停下来时间为 小时;
(3)甲从出发起,经过 小时与乙相遇;
(4)甲行走的平均速度是多少千米小时?
【考点】
通过函数图象获取信息;
基础巩固
能力提升
变式训练
拓展培优
真题演练