1.
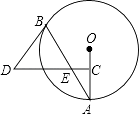
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合).

(1)
若CM=2,
(2)
在(1)的条件下,求点P到AB边的距离的最小值,并求出当取得这个最小值时,点P运动路线的长是多少?(参考数据:sin54°=cos36°≈  ,sin36°=cos54°≈
,sin36°=cos54°≈  ,结果保留π)
(3)
设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围.
,结果保留π)
(3)
设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围.
①又当点N在CB上,MP∥BC时,则CN=,MN=;
【考点】
直线与圆的位置关系;