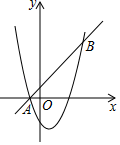
一个装满水的水杯竖直放置在水平桌面上时的纵向截面如图所示，其左右轮廓线、都是抛物线的一部分，已知水杯底部宽为，水杯高度为，杯口直径为且，以杯底的中点为原点，以为轴，的垂直平分线为轴建立平面直角坐标系．（1）轮廓线、所在的抛物线的解析式为：；（2）将水杯绕点倾斜倒出部分水，杯中水面，如图当倾斜角时，水面宽度为

0 返回首页

1. 一个装满水的水杯竖直放置在水平桌面 $\text{[math]}$ 上时的纵向截面如图 $\text{[math]}$ 所示，其左右轮廓线 $\text{[math]}$ 、 $\text{[math]}$ 都是抛物线 $\text{[math]}$ 的一部分，已知水杯底部 $\text{[math]}$ 宽为 $\text{[math]}$ ，水杯高度为 $\text{[math]}$ ，杯口直径 $\text{[math]}$ 为 $\text{[math]}$ 且 $\text{[math]}$ ，以杯底 $\text{[math]}$ 的中点为原点 $\text{[math]}$ ，以 $\text{[math]}$ 为 $\text{[math]}$ 轴， $\text{[math]}$ 的垂直平分线为 $\text{[math]}$ 轴建立平面直角坐标系．

（1）轮廓线 $\text{[math]}$ 、 $\text{[math]}$ 所在的抛物线 $\text{[math]}$ 的解析式为：；

（2）将水杯绕点 $\text{[math]}$ 倾斜倒出部分水，杯中水面 $\text{[math]}$ ，如图 $\text{[math]}$ 当倾斜角 $\text{[math]}$ 时，水面宽度为 $\text{[math]}$ $\text{[math]}$

【考点】

待定系数法求二次函数解析式; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 已知一条抛物线的形状、开口方向均与抛物线 $\text{[math]}$ 相同，且它的顶点坐标为 $\text{[math]}$ ，则这条抛物线的解析式为．

填空题容易

2. 若一个二次函数的二次项系数为2，且经过点 $\text{[math]}$ ，请写出一个符合上述条件的二次函数表达式：．

填空题容易

3. 已知抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，它的对称轴是直线 $\text{[math]}$ ，则这条抛物线的函数表达式是．

填空题容易

1. 某厂家特制了一批高脚杯，分为男士杯和女士杯（如图1），相关信息如下：

素材	内容
素材1	如图1，这种高脚杯从下往上分为三部分：杯托，杯脚，杯体．杯托为一个圆，水平放置时候，杯脚经过杯托圆心，并垂直任意直径，杯体的水平横截面都为圆，这些圆的圆心都在杯脚所在直线上．
素材2	图2坐标系中，特制男士杯可以看作由线段 $\text{[math]}$ ， $\text{[math]}$ ，抛物线 $\text{[math]}$ （实线部分），线段 $\text{[math]}$ ，线段 $\text{[math]}$ 绕 $\text{[math]}$ 轴旋转形成的立体图形（不考虑杯子厚度，下同）；特制女士杯可以看作由线段 $\text{[math]}$ ， $\text{[math]}$ ，抛物线 $\text{[math]}$ （虚线部分）绕 $\text{[math]}$ 轴旋转形成的立体图形
素材3	已知，图2坐标系中， $\text{[math]}$ ，记为 $\text{[math]}$ ， $\text{[math]}$ ．

根据以上素材内容，尝试求解以下问题：

(1) 求抛物线 $\text{[math]}$ 和抛物线 $\text{[math]}$ 的解析式；

(2) 当杯子水平放置及杯内液体静止时，若男士杯中的液体与女士杯中的液体深度均为4cm，求两者液体最上层表面圆面积之差；（结果保留 $\text{[math]}$ ）

(3) 当杯子水平放置及杯内液体静止时，若男士杯中的液体与女士杯中的液体深度相等，两者液体最上层表面圆面积相差 $\text{[math]}$ ，求杯中液体的深度．

综合题普通

2. 已知抛物线y＝ax²+bx+3的顶点坐标为（﹣1，4），与x轴交于点A和点B ，与y轴交于点C ，点P为第二象限内抛物线上的动点．

(1) 求抛物线的解析式；

(2) 如图1，连接OP交BC于点D ，当S_△_CPD：S_△_BPD＝1：2时，请求出点D的坐标；

(3) 如图2，点E的坐标为（0，﹣1），点G为x轴负半轴上的一点，∠OGE＝15°，连接PE ，若∠PEG＝2∠OGE ，请求出点P的坐标；

综合题困难

3. 2024年3月4日，跳水世界杯蒙特利尔站女子十米台，中国队选手包揽冠亚军，出色的表现，再次向世界展示了中国跳水队的卓越实力．如图，建立平面直角坐标系xOy．如果运动员从点A起跳后的运动路线可以看作抛物线的一部分，那么从起跳到入水的过程中，她的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系式 $\text{[math]}$ ．

(1) 在平时训练完成一次跳水动作时，运动员的水平距离x与竖直高度y的几组数据如下：

水平距离 $\text{[math]}$	3	3.5	4	4.5
竖直高度 $\text{[math]}$	10	__________	__________	6.25

①求抛物线的解析式．

②补全表格．

(2) 信息一：运动员起跳后达到最高点B，点B到水面的高度为km，从到达最高点B开始计时，则她到水面的距离 $\text{[math]}$ 与时间 $\text{[math]}$ 之间满足 $\text{[math]}$ ．

信息二：已知运动员在到达最高点后，在落水前至少需要 $\text{[math]}$ 的时间才能完成极具难度的跳水动作．

①请通过计算说明，在（1）的这次训练中1，运动员能否顺利完成极具难度的跳水动作？

②运动员进行第二次跳水训练，此时她们竖直高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 的关系为 $\text{[math]}$ ．若她在到达最高点后要顺利完成极具难度的跳水动作，则n的取值范围是__________ ．

综合题普通

1. 已知抛物线y＝ax²+2x+c（a≠0）与x轴交于点A（﹣1，0）和点B，与直线y＝﹣x+3交于点B和点C，M为抛物线的顶点，直线ME是抛物线的对称轴．

（1）求抛物线的解析式及点M的坐标；

（2）直线ME与BC交于点N，点P为直线BC上方抛物线上一点，在直线BC上是否存在一点Q，使得以点M、N、P、Q为顶点的四边形是平行四边形，若存在，请求出点Q的坐标；

（3）点F为直线BC上一点，作点A关于y轴的对称点A'，连接A'C，A'F，当△FA'C是直角三角形时，直接写出点F的坐标．

解答题普通

2. 如图，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，其顶点为 $\text{[math]}$ ，对称轴是直线 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

（1）求该抛物线的解析式；

（2）若点 $\text{[math]}$ 是该抛物线对称轴 $\text{[math]}$ 上的一个动点，求 $\text{[math]}$ 周长的最小值；

（3）如图（2），若 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点 $\text{[math]}$ $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 不重合），过 $\text{[math]}$ 点作平行于 $\text{[math]}$ 轴的直线交抛物线于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ．

①求 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；

② $\text{[math]}$ 是否存在最大值？若存在，求出最大值及此时点 $\text{[math]}$ 的坐标；若不存在，请说明理由．

解答题困难

3. 抛物线 $\text{[math]}$ 的图象经过点A( 1，0)，B(0，5)．

（1）求这个抛物线的解析式；

（2）设（1）中的抛物线与 $\text{[math]}$ 轴的另一交点为C，抛物线的顶点为D，试求出 $\text{[math]}$ 的面积；

（3） $\text{[math]}$ 是线段 $\text{[math]}$ 上的一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，与抛物线交于 $\text{[math]}$ 点，若直线 $\text{[math]}$ 把 $\text{[math]}$ 分成面积之比为 $\text{[math]}$ 的两部分，请求出 $\text{[math]}$ 点的坐标．