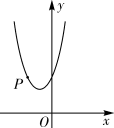
2024年3月4日，跳水世界杯蒙特利尔站女子十米台，中国队选手包揽冠亚军，出色的表现，再次向世界展示了中国跳水队的卓越实力．如图，建立平面直角坐标系xOy．如果运动员从点A起跳后的运动路线可以看作抛物线的一部分，那么从起跳到入水的过程中，她的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系式．

1. 2024年3月4日，跳水世界杯蒙特利尔站女子十米台，中国队选手包揽冠亚军，出色的表现，再次向世界展示了中国跳水队的卓越实力．如图，建立平面直角坐标系xOy．如果运动员从点A起跳后的运动路线可以看作抛物线的一部分，那么从起跳到入水的过程中，她的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系式 $\text{[math]}$ ．

(1) 在平时训练完成一次跳水动作时，运动员的水平距离x与竖直高度y的几组数据如下：

水平距离 $\text{[math]}$	3	3.5	4	4.5
竖直高度 $\text{[math]}$	10	__________	__________	6.25

①求抛物线的解析式．

②补全表格．

(2) 信息一：运动员起跳后达到最高点B，点B到水面的高度为km，从到达最高点B开始计时，则她到水面的距离 $\text{[math]}$ 与时间 $\text{[math]}$ 之间满足 $\text{[math]}$ ．

信息二：已知运动员在到达最高点后，在落水前至少需要 $\text{[math]}$ 的时间才能完成极具难度的跳水动作．

①请通过计算说明，在（1）的这次训练中1，运动员能否顺利完成极具难度的跳水动作？

②运动员进行第二次跳水训练，此时她们竖直高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 的关系为 $\text{[math]}$ ．若她在到达最高点后要顺利完成极具难度的跳水动作，则n的取值范围是__________ ．

【考点】

待定系数法求二次函数解析式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，小车从点A出发，沿与水平面成 $\text{[math]}$ 角光滑斜坡 $\text{[math]}$ 下滑，在下滑过程中小车速度逐渐增加，设小车出发点A离水平地面 $\text{[math]}$ 的高度为h，小车从点A滑行到最低点B所用的时间为t（秒），小车滑行到点B时的速度为v（厘米/秒）．速度v与时间t满足关系： $\text{[math]}$ ，高度h与时间t满足关系： $\text{[math]}$ （ $\text{[math]}$ ， g是常数），当小车出发点小车出发点A离水平地面 $\text{[math]}$ 的高度为20（厘米）时，小车从点A滑到最低点B需要2秒．

(1) 当小车出发点A离水平地面 $\text{[math]}$ 的高度为45（厘米）时，小车滑到最低点B需要几秒钟？此时小车到达B点时的速度是多少？

(2) 小车继续在粗糙的水平地面 $\text{[math]}$ 上滑行，设滑行的距离为s（厘米），小车从斜坡滑行到点B时速度为v（厘米/秒），小车在水平地面 $\text{[math]}$ 上滑行的时间为T（秒），若s与v，T之间满足以下关系： $\text{[math]}$ （ $\text{[math]}$ ， a是常数），当 $\text{[math]}$ （厘米/秒）时， $\text{[math]}$ （厘米）， $\text{[math]}$ （秒）．如果把小车出发点A离水平地面 $\text{[math]}$ 的距离h提高到125厘米，那么当滑行到时间 $\text{[math]}$ 秒时，小车在水平地面 $\text{[math]}$ 上滑行的距离为多少？

综合题普通

2. 小明周末来到小湖边玩打水漂的游戏，打出的水漂呈抛物线形状．小明站在岸边向湖中抛出一个石片，石片在距离小明 $\text{[math]}$ 远的水面重新弹了起来，当石片运动到距小明 $\text{[math]}$ 时，达到了最大高度 $\text{[math]}$ ，以小明所在的位置为原点，建立如图所示的平面直角坐标系，设抛物线的表达式为 $\text{[math]}$ ，其中 $\text{[math]}$ 是石片距小明的水平距离， $\text{[math]}$ 是石片距水面的高度．

(1) 求抛物线的表达式；

(2) 若在距离小明 $\text{[math]}$ 的水面上有5艘小艇并排紧靠着，每艘小艇的高度为 $\text{[math]}$ ，宽度为 $\text{[math]}$ （小艇之间的间隙及浮力忽略不计），则石片在弹起运行的过程中，能否越过这5艘小艇重新落入水中？

综合题普通

3. 如图①，地面 $\text{[math]}$ 上两根等长立柱 $\text{[math]}$ ， $\text{[math]}$ 之间悬挂一根近似成抛物线 $\text{[math]}$ 的绳子．

(1) 求绳子最低点到地面的距离．

(2) 如图②，因实际需要，需用一根立柱 $\text{[math]}$ 撑起绳子．

①若在离 $\text{[math]}$ 的4米位置处用立柱 $\text{[math]}$ 撑起，使立柱左侧的抛物线的最低点距 $\text{[math]}$ 的距离为1米，离地面1.8米，求 $\text{[math]}$ 的长；

②将立柱 $\text{[math]}$ 来回移动，移动过程中，在一定范围内，总保持立柱 $\text{[math]}$ 左侧抛物线的形状不变，其函数表达式为 $\text{[math]}$ ，当抛物线最低点到地面距离为 $\text{[math]}$ 米时，求m的值．

综合题普通