1.
互动学习课堂上,某小组同学对一个课题展开了探究.
(1)
已知:如图,在 中,
中, 和
和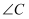 的平分线相交于点P,试探究
的平分线相交于点P,试探究 和
和 的关系.请在以下解答过程的空白处填上适当的内容(理由成数学式).
(2)
如图,在
的关系.请在以下解答过程的空白处填上适当的内容(理由成数学式).
(2)
如图,在 中,
中, 的平分线和外角
的平分线和外角 的平分线相交于点P,试探究
的平分线相交于点P,试探究 和
和 的关系,并说明理由.
(3)
如图,
的关系,并说明理由.
(3)
如图, 的外角
的外角 的平分线和
的平分线和 的平分线相交于点P,若
的平分线相交于点P,若 , 则
, 则 的度数为__________.
的度数为__________.

解:延长交
于点D.
,
(__________),
.
和
的平分线相交于点P,
,
(角平分线定义),
.
(__________),
(等式的性质),
__________.


【考点】
三角形内角和定理;
角平分线的性质;
能力提升
真题演练