1.
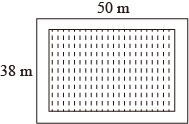
如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.

【考点】
一元二次方程的应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练