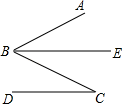
综合与实践【问题情境】在综合与实践课上，同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动．如图1，已知两直线a，b且和，，，．（1）在图1中，，求的度数；【深入探究】（2）如图2，创新小组的同学把直线a向上平移，并把的位置改变，发现，请说明理由；【拓展应用】（3）缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，平分，此时发现与又存在新的数量关系，请直接写出与的数量关系．

1. 在数学活动课上，老师组织七（8）班的同学开展了探究两角之间数量关系的数学活动．如图，已知射线 $\text{[math]}$ ，连接 $\text{[math]}$ ，点P是射线 $\text{[math]}$ 上一动点（与点A不重合）， $\text{[math]}$ 、 $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ，分别交射线 $\text{[math]}$ 于点C，D．

【小试牛刀】

（1）①若 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数；

②若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为____________．(用含 x的代数式表示）

【变式探索】

（2）当点P运动时， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．

【能力提升】

（3）当点P运动到使 $\text{[math]}$ 时， $\text{[math]}$ _________（直接写出结果）．

解答题容易

2. ．完成下面的证明．

已知：如图，三角形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．

求证： $\text{[math]}$ 是 $\text{[math]}$ 的角平分线．

证明：∵ $\text{[math]}$ ，

$\text{[math]}$ （_______），

$\text{[math]}$ ，

$\text{[math]}$ _______，

$\text{[math]}$ 是 $\text{[math]}$ 的角平分线（_______）．

证明题容易

3. 如图， $\text{[math]}$ ，且 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

计算题容易

1. 如图1，已知 $\text{[math]}$ ， C为射线 $\text{[math]}$ 上一点(不与点A 重合)，连接 $\text{[math]}$

【发现】如图2过点C作 $\text{[math]}$

（1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

【探究】直接写出图1中 $\text{[math]}$ 和 $\text{[math]}$ 之间的数量关系：；

【拓展】利用【探究】中的结论完成下列问题．

如图3， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点(不与点A 重合)，在射线 $\text{[math]}$ 上取一点O，过点O作直线 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点E， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点F， $\text{[math]}$ 交 $\text{[math]}$ 于点G，当点C沿着射线 $\text{[math]}$ 方向运动时， $\text{[math]}$ 的度数是否会变化？若变化，请说明理由；若不变，请求出这个不变的值．

实践探究题普通

2. 如图， $\text{[math]}$ ，定点E，F分别在直线 $\text{[math]}$ 上，在平行线 $\text{[math]}$ 之间有一动点P，满足 $\text{[math]}$ ．

(1) 试问 $\text{[math]}$ 满足怎样的数量关系？

解：由于点P是平行线 $\text{[math]}$ 之间有一动点，因此需要对点P的位置进行分类讨论：

如图1，当P点在 $\text{[math]}$ 的左侧时， $\text{[math]}$ 满足数量关系为，

如图2，当P点在 $\text{[math]}$ 的右侧时， $\text{[math]}$ 满足数量关系为．

(2) 如图3， $\text{[math]}$ 分别平分 $\text{[math]}$ 和 $\text{[math]}$ ，且点P在 $\text{[math]}$ 左侧．

①若 $\text{[math]}$ ，则 $\text{[math]}$ 　　．

②猜想 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；

③如图4，若 $\text{[math]}$ 与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ；此次类推，则 $\text{[math]}$ 与 $\text{[math]}$ 满足怎样的数量关系？（直接写出结果）

(3) 【拓展应用】如图5，已知 $\text{[math]}$ ，点E在直线 $\text{[math]}$ 上，点P在直线 $\text{[math]}$ 上方，连接 $\text{[math]}$ ， $\text{[math]}$ 的角平分线与 $\text{[math]}$ 的角平分线所在直线交于点Q，则 $\text{[math]}$ ＝　　°．

实践探究题困难

3. 综合与实践数学社团的同学以“两条平行线 $\text{[math]}$ ， $\text{[math]}$ 和一块含 $\text{[math]}$ 角的直角三角板 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）”为主题开展数学活动，已知点E、F不能同时落在直线 $\text{[math]}$ 和 $\text{[math]}$ 之间．

(1) 观察猜想：如图1，把三角板的 $\text{[math]}$ 角的顶点E，G 分别放在 $\text{[math]}$ ， $\text{[math]}$ 上，若 $\text{[math]}$ $\text{[math]}$ 则 $\text{[math]}$ 的度数为；

(2) 类比探究：如图2，把三角板的锐角顶点 G 放在 $\text{[math]}$ 上，且保持不动，绕点 G 转动三角板，若点E恰好落在 $\text{[math]}$ 和 $\text{[math]}$ 之间，且 $\text{[math]}$ 与 $\text{[math]}$ 所夹锐角为 $\text{[math]}$ （即 $\text{[math]}$ $\text{[math]}$ 求 $\text{[math]}$ 的度数；

(3) 解决问题：把三角板的锐角顶点G放在 $\text{[math]}$ 上，在绕点G旋转三角板的过程中，若存在 $\text{[math]}$ ( $\text{[math]}$ )，请求出射线 $\text{[math]}$ 与 $\text{[math]}$ 相交所夹锐角的度数．

实践探究题普通

1. 如图， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；②

$\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤若 $\text{[math]}$ ，则 $\text{[math]}$ ．其中正确结论的个数是（　　）

A. 2个 B. 3个 C. 4个 D. 5个

单选题普通

2. 如图，已知 $\text{[math]}$ ， FC平分 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. 20° B. 35° C. 45° D. 70°

单选题普通

3. 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 度．

填空题容易

1. 已知， $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 M，交 $\text{[math]}$ 于点 N，（ $\text{[math]}$ 点 E 是线段 $\text{[math]}$ 上一点（不与 M、N重合）， P、Q分别是射线 $\text{[math]}$ 、 $\text{[math]}$ 上异于端点的点，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点F， $\text{[math]}$ 平分 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 G．

(1) 如图1， $\text{[math]}$ ， $\text{[math]}$ ，点 G在线段 $\text{[math]}$ 上．

①求 $\text{[math]}$ 的度数；

②求 $\text{[math]}$ 的度数；

(2) 试探索 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；

(3) 已知 $\text{[math]}$ ．直线 $\text{[math]}$ 、 $\text{[math]}$ 交于点K，直线 $\text{[math]}$ 从与直线 $\text{[math]}$ 重合的位置开始绕点N顺时针旋转，旋转速度为每秒 $\text{[math]}$ ，当 $\text{[math]}$ 首次与直线 $\text{[math]}$ 重合时，运动停止，在此运动过程中，经过t秒， $\text{[math]}$ 恰好平行于 $\text{[math]}$ 的其中一条边，请直接写出所有满足条件的t的值．

解答题困难

2. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为射线 $\text{[math]}$ 上一动点，过点 $\text{[math]}$ 向射线 $\text{[math]}$ 的右侧作射线 $\text{[math]}$ ，使 $\text{[math]}$ ，作 $\text{[math]}$ 的平分线 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ．