已知二次函数y=ax2+bx+2的图象经过点A（2，2）．

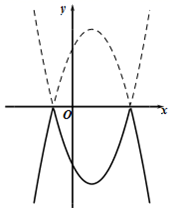
1. 已知二次函数y=ax²+bx+2的图象经过点A（2，2）．

(1) 若直线y=x与抛物线 $\text{[math]}$ 相交所得的线段长为 $\text{[math]}$ 求a的值：

(2) 若抛物线y=ax²+bx+2与x轴交于M（x₁ ， 0）和N（x₂ ， 0）两点（x₁＜x₂），且2x₁+x₂＞0，直接写出a的取值范围．

【考点】

二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 随着科技的发展，扫地机器人（图1）已广泛应用于生活中．某公司推出一款新型扫地机器风，经统计该产品2022年每个月的销售情况发现，每台的销售价格随销售月份的变化而变化设该产品2022年第x（x为整数）个月每台的销售价格为y（单位：元），y 与x的函数关系如图2所示（图中ABC为一折线）．

(1) 当1≤x≤10时，求每台的销售价格y与x之间的函数关系热．

(2) 设该产品2022年第x个月的销售数量为m（单位：万台），m与x的关系可以用m= $\text{[math]}$ x+1来描述，求哪个月的销售收入最多，最多为多少万元？（销售收入=每台的销售价格×销售数量）

解答题普通

2. 在平面直角坐标系xOy中，抛物线y＝mx²+2mx﹣3m+2．

(1) 求抛物线的对称轴；

(2) ①过点P（0，2）作与x轴平行的直线，交抛物线于点M ， N ．求点M ， N的坐标；

②横、纵坐标都是整数的点叫做整点．如果抛物线和线段MN围成的封闭区域内（不包括边界）恰有3个整点，求m的取值范围．

解答题困难

3. 已知反比例函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 和点 $\text{[math]}$ ．

(1) 求这两个函数的关系式．

(2) 结合图象直接比较：当 $\text{[math]}$ 时，根据自变量：x的取值范围比较 $\text{[math]}$ 和 $\text{[math]}$ 的大小．

解答题普通