1.
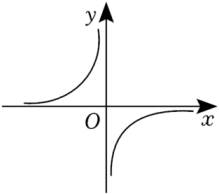
反比例函数 的图象经过点
的图象经过点 , 则下列说法错误的是( )
, 则下列说法错误的是( )
A.
 B.
函数图象分布在第二、四象限
C.
函数图象关于原点中心对称
D.
当
B.
函数图象分布在第二、四象限
C.
函数图象关于原点中心对称
D.
当 时,
时, 随
随 的增大而减小
的增大而减小
【考点】
反比例函数的图象;
反比例函数的性质;