定义：如图1，在平面直角坐标系中，点是平面内任意一点（坐标轴上的点除外），过点分别作轴、轴的垂线，若由点、原点、两个垂足、为顶点的矩形的周长与面积的数值相等时，则称点是平面直角坐标系中的“美好点”．

1. 定义：如图1，在平面直角坐标系中，点 $\text{[math]}$ 是平面内任意一点（坐标轴上的点除外），过点 $\text{[math]}$ 分别作 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的垂线，若由点 $\text{[math]}$ 、原点 $\text{[math]}$ 、两个垂足 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的矩形 $\text{[math]}$ 的周长与面积的数值相等时，则称点 $\text{[math]}$ 是平面直角坐标系中的“美好点”．

(1) 【尝试初探】

点 $\text{[math]}$ “美好点”（填“是”或“不是” $\text{[math]}$ ；若点 $\text{[math]}$ 是第一象限内的一个“美好点”，则 $\text{[math]}$ ；

(2) 【深入探究】

若“美好点” $\text{[math]}$ ， $\text{[math]}$ 在双曲线 $\text{[math]}$ ，且 $\text{[math]}$ 为常数）上，则 $\text{[math]}$ ；

(3) 【拓展延伸】

我们可以从函数的角度研究“美好点”，已知点 $\text{[math]}$ 是第一象限内的“美好点”．

①求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式，并求出自变量 $\text{[math]}$ 的取值范围；

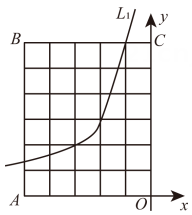
②在图2的平面直角坐标系中画出函数图象：

列表：下表是 $\text{[math]}$ 与 $\text{[math]}$ 的几组对应值，请将下表填写完整．

$\text{[math]}$	$\text{[math]}$	3	4	5	6	7	8	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$							$\text{[math]}$

描点：根据表中各组对应值 $\text{[math]}$ ，在图2的平面直角坐标系中描出各点；

连线：用平滑的曲线顺次连接各点，画出函数图象；

③结合图象研究性质，下列结论正确的选项是 ▲ ；（多项选择，全部选对的得2分，部分选对的得1分，有选错的不得分）

$\text{[math]}$ ．图象与经过点 $\text{[math]}$ 且平行于坐标轴的直线没有交点；

$\text{[math]}$ ． $\text{[math]}$ 随着 $\text{[math]}$ 的增大而减小；

$\text{[math]}$ ． $\text{[math]}$ 随着 $\text{[math]}$ 的增大而增大；

$\text{[math]}$ ．图象经过点 $\text{[math]}$ ．

④对于图象上任意一点 $\text{[math]}$ ，代数式 $\text{[math]}$ 是否为定值？如果是，请求出这个定值，如果不是，请说明理由．

⑤结合上述问题，观察图象可知该图象可由哪个函数 $\text{[math]}$ 的图象怎样平移得到？

【考点】

反比例函数的图象; 反比例函数的性质; 矩形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

1. 如图，矩形ABCO在平面直角坐标系中，点A(-5，0)，C(0，6)，反比例函数图象 L₁ 对应的函数表达式为 $\text{[math]}$ 反比例函数图象 L₂ 对应的函数表达式为 $\text{[math]}$ 把矩形 ABCO内部(不含边界)横、纵坐标均为整数的点称为“整点”.

(1) 若 k=-12，则L₂和L₁ 之间(不含边界)有个“整点”.

(2) 若L₂ 和L₁之间(不含边界)有4个“整点”，求k的取值范围.

实践探究题困难

2. 探究函数y=x+ $\text{[math]}$ 的图象与性质

(1) 函数y=x+ $\text{[math]}$ 的自变量x的取值范围是；

下列四个函数图象中，函数y=x+ $\text{[math]}$ 的图象大致是

(3) 对于函数y=x+ $\text{[math]}$ ，求当x＞0时，y的取值范围．

请将下面求解此问题的过程补充完整：

解：∵x＞0

∴y=x+ $\text{[math]}$

=（ $\text{[math]}$ ）²+（ $\text{[math]}$ ）²

=（ $\text{[math]}$ ﹣ $\text{[math]}$ ）²+

∵（ $\text{[math]}$ ﹣ $\text{[math]}$ ）²≥0，

∴y．

(4) 若函数y= $\text{[math]}$ ，则y的取值范围是

实践探究题普通