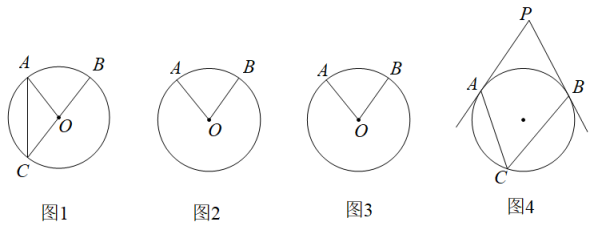
1.
如图,在 中,
中, , 以
, 以 为直径的
为直径的 交边
交边 于点
于点 , 连接
, 连接 , 过点
, 过点 作
作 .
.

(1)
请完成作图:过点 作
作 的切线,交
的切线,交 于点
于点 ;
(2)
在(1)的条件下,求证:
;
(2)
在(1)的条件下,求证: ;
(3)
在(1)的条件下,
;
(3)
在(1)的条件下, ,
,  , 求⊙O的半径.
, 求⊙O的半径.
【考点】
圆的综合题;