1.
(1)
课本再现:在 中,
中, 是
是 所对的圆心角,
所对的圆心角, 是
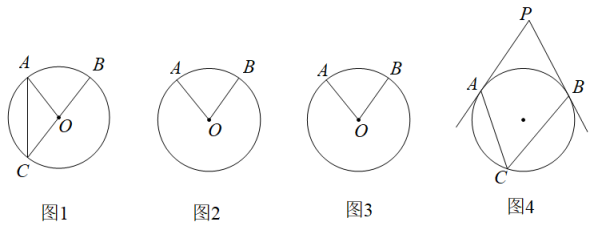
是 所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与
所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与 的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其它两种情况的图形,并从三种位置关系中任选一种情况证明
的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其它两种情况的图形,并从三种位置关系中任选一种情况证明 ;
(2)
知识应用:如图4,若
;
(2)
知识应用:如图4,若 的半径为2,
的半径为2, 分别与
分别与 相切于点A,B,
相切于点A,B, , 求
, 求 的长.
的长.
【考点】
圆周角定理;
切线的性质;
圆的综合题;
能力提升
真题演练