1.
【问题情境】
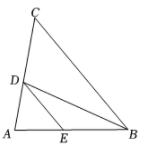
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线 , 连接AB , 点P是射线AM上的一个动点(与点A不重合),BC , BD分别平分
和
, 分别交射线AM于点C、D.

(1)
【初步探究】
(2)
不断改变 的度数,
的度数, 与
与 始终存在某种数量关系,用含
始终存在某种数量关系,用含 的式子表示
的式子表示 ;
(3)
【类比探究】“智慧小组”发现,当点P在AM上继续运动到使
;
(3)
【类比探究】“智慧小组”发现,当点P在AM上继续运动到使 时,
时, 的结果是一个定值,请你帮助探究并说明理由.
的结果是一个定值,请你帮助探究并说明理由.
“快乐小组”经过探索后发现:
当时,试说明
;
【考点】
平行线的性质;
角平分线的概念;
能力提升
真题演练