1.
定义：对角线互相垂直的四边形叫做“垂美”四边形．
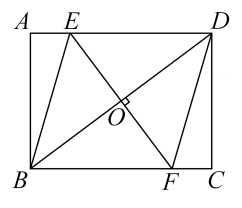
了解性质：如图1：已知四边形ABCD中，AC⊥BD ． 垂足为O ， 则有：AB2+CD2＝AD2+BC2；
（图1） （图2） （图3）
（图4） （图5）
(1)
性质应用：如图1，四边形ABCD是垂美四边形，若AD=2，BC=4，CD=3，则AB=；
(2)
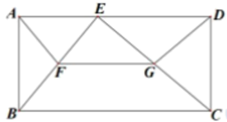
性质变式：如图2，图3，P是矩形ABCD所在平面内任意一点，则有以下重要结论：AP2+CP2＝BP2+DP2 ． 请以图3为例将重要结论证明出来．
(3)
应用变式：①如图4，在矩形ABCD中，O为对角线交点，P为BO中点，则
；(写出证明过程）
②如图5，在∆ABC中，CA=4，CB=6，D是∆ABC内一点，且CD=2，∠ADB=90°，则AB的最小值是．
【考点】
勾股定理;
矩形的性质;
