1.
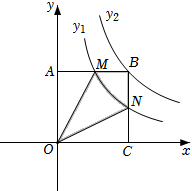
如图, 点  在双曲线
在双曲线  上, 点
上, 点  在双曲线
在双曲线  上,
上,  轴, 点
轴, 点  是
是  轴上一点, 连结
轴上一点, 连结  , 若
, 若  的面积是 6 , 则
的面积是 6 , 则  的值为( )
的值为( )

A.
-6
B.
-8
C.
-10
D.
-12
【考点】
反比例函数系数k的几何意义;