1.
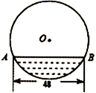
唐代李皋发明了“桨轮船”,他设计的桨轮船在船的舷侧或尾部装有带有桨叶的桨轮,通过人力踩动桨轮轴来推动船体前进.这种船的桨轮下半部浸入水中,上半部露出水面,因其推进方式类似车轮,故又被称为“明轮船”或“轮船”.如图,该桨轮船的轮子被水面截得线段 为
为 , 轮子的吃水深度为
, 轮子的吃水深度为 , 则该桨轮船轮子半径为( )
, 则该桨轮船轮子半径为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
垂径定理的实际应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练