1.
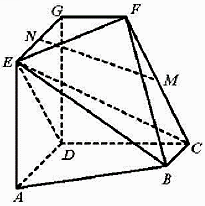
如图,正方体 的棱长为3,点E在棱
的棱长为3,点E在棱 上,点F在棱
上,点F在棱 上,G在棱
上,G在棱 上,且
上,且 , H是棱
, H是棱 上一点.
上一点.

(1)
求证:E,B,F,D四点共面;
(2)
若平面 平面
平面 , 求证:H为
, 求证:H为 的中点.
的中点.
【考点】
直线与平面平行的性质;