如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．

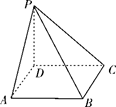
1. 如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．

(1) 证明：l⊥平面PDC；

(2) 已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．

【考点】

直线与平面平行的判定; 直线与平面平行的性质; 直线与平面垂直的判定; 用空间向量研究直线与平面所成的角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图所示，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 为平行四边形，侧面 $\text{[math]}$ 为正三角形， $\text{[math]}$ 为线段 $\text{[math]}$ 上一点， $\text{[math]}$ 为 $\text{[math]}$ 的中点.

(1) 当 $\text{[math]}$ 为 $\text{[math]}$ 的中点时，求证： $\text{[math]}$ 平面 $\text{[math]}$ .

(2) 当 $\text{[math]}$ 平面 $\text{[math]}$ ，求出点 $\text{[math]}$ 的位置，说明理由.

解答题普通

2. 如图，多面体ABCDEF的面ABCD是正方形，其中心为M．平面 $\text{[math]}$ 平面ABCD， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 平面AEFB；

(2) 在 $\text{[math]}$ 内（包括边界）是否存在一点N，使得 $\text{[math]}$ 平面CEF？若存在，求点N的轨迹，并求其长度；若不存在，请说明理由．

解答题普通

3. 已知 $\text{[math]}$ 的斜边为AB，过点A作PA⊥平面ABC，AM⊥PB于M，AN⊥PC于N.求证：

(1) BC⊥平面PAC；

(2) PB⊥平面AMN.

解答题普通