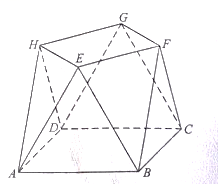
如图，多面体ABCDEF的面ABCD是正方形，其中心为M．平面平面ABCD，，，．

1. 如图，多面体ABCDEF的面ABCD是正方形，其中心为M．平面 $\text{[math]}$ 平面ABCD， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 平面AEFB；

(2) 在 $\text{[math]}$ 内（包括边界）是否存在一点N，使得 $\text{[math]}$ 平面CEF？若存在，求点N的轨迹，并求其长度；若不存在，请说明理由．

【考点】

直线与平面平行的判定; 直线与平面垂直的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知 $\text{[math]}$ 的斜边为AB，过点A作PA⊥平面ABC，AM⊥PB于M，AN⊥PC于N.求证：

(1) BC⊥平面PAC；

(2) PB⊥平面AMN.

解答题普通

2. 在直三棱柱 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P，Q，R分别是棱 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点．

(1) 求证： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 求证：直线 $\text{[math]}$ 平面 $\text{[math]}$ ．

解答题普通

3. 如图所示，在正方体 $\text{[math]}$ 中， $\text{[math]}$ 分别为 $\text{[math]}$ ､ $\text{[math]}$ 的中点.

(1) 求证： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 求证： $\text{[math]}$ 平面 $\text{[math]}$ .

解答题普通