1.
设抛物线 的焦点为
的焦点为 , 已知点
, 已知点 到圆
到圆 上一点的距离的最大值为6.
上一点的距离的最大值为6.
(1)
求抛物线 的方程.
(2)
设
的方程.
(2)
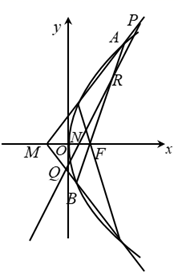
设 是坐标原点,点
是坐标原点,点 是抛物线
是抛物线 上异于点
上异于点 的两点,直线
的两点,直线 与
与 轴分别相交于
轴分别相交于 两点(异于点
两点(异于点 ),且
),且 是线段
是线段 的中点,试判断直线
的中点,试判断直线 是否经过定点.若是,求出该定点坐标;若不是,说明理由.
是否经过定点.若是,求出该定点坐标;若不是,说明理由.
【考点】
抛物线的标准方程;
直线与圆锥曲线的综合问题;