1.
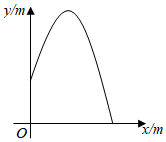
某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根顶部带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心的水平距离也为3m,那么水管的设计高度应 为
【考点】
二次函数的实际应用-喷水问题;
能力提升
变式训练
拓展培优
真题演练