1.
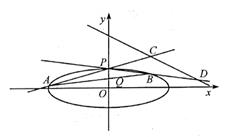
在直角坐标系 中,已知椭圆
中,已知椭圆 的左右焦点分别为
的左右焦点分别为 ,
,  , 离心率是
, 离心率是 , 点P为椭圆短轴的一个端点,
, 点P为椭圆短轴的一个端点, 的面积是
的面积是 .
.
(1)
求椭圆的方程;
(2)
若动直线l与椭圆E交于A,B两点,且恒有 , 是否存在一个以原点O为圆心的定圆,使得动直线l始终与定圆相切?若存在,求出圆的方程,若不存在,请说明理由.
, 是否存在一个以原点O为圆心的定圆,使得动直线l始终与定圆相切?若存在,求出圆的方程,若不存在,请说明理由.
【考点】
直线与圆锥曲线的综合问题;