1.
某研究小组设计了一种“用一把刻度尺测量质量为 的小物块
的小物块 与平板
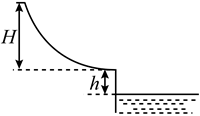
与平板 之间动摩擦因数”的实验方案,实验装置如图甲所示.
之间动摩擦因数”的实验方案,实验装置如图甲所示.

是半径足够大的四分之一圆弧轨道,与水平固定放置
板的上表面
在
点相切,
点在水平地面的垂直投影为
重力加速度为
实验步骤如下:
用刻度尺测量
长度为
和
高度为
;
先不放置平板
如图乙
使圆弧
的末端
位于
的正上方,将物块
在
点由静止释放,在物块
落地处标记其落地点
;
重复步骤
, 共做
次;
用半径尽量小的圆将
个落地点围住,用毫米刻度尺测量圆心到
的距离
;
放置平板
如图甲
, 将物块
由同一位置
由静止释放,在物块
落地处标记其落地点
;
重复步骤
, 共做
次;
用半径尽量小的圆将
个落地点围住,用毫米刻度尺测量圆心到
的距离
.
(1)
实验步骤 目的是.
(2)
用实验中的测量量表示:物块
目的是.
(2)
用实验中的测量量表示:物块 滑到
滑到 点时的动能
点时的动能 .
(3)
物块
.
(3)
物块 与平板
与平板 之间的动摩擦因数
之间的动摩擦因数 .
(4)
已知实验测得的
.
(4)
已知实验测得的 值与实际值不等,其原因除了实验中测量的误差之外,其他的原因可能是
值与实际值不等,其原因除了实验中测量的误差之外,其他的原因可能是 写出一个可能的原因即可
写出一个可能的原因即可 .
.
【考点】
平抛运动;
动能定理的综合应用;
能力提升
真题演练