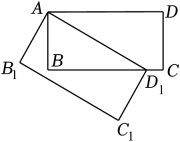
如图，嘉嘉在A时测得一棵高的树的影长为，若A时和B时两次日照的光线互相垂直，则B时的影长为（）

0 返回出卷网首页

1. 如图，嘉嘉在A时测得一棵 $\text{[math]}$ 高的树的影长 $\text{[math]}$ 为 $\text{[math]}$ ，若A时和B时两次日照的光线互相垂直，则B时的影长 $\text{[math]}$ 为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

勾股定理的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 一个圆桶底面直径为24cm，高32cm，则桶内所能容下的最长木棒为（　　）

A. 20cm B. 50cm C. 40cm D. 45cm

单选题容易

2. 如图，将矩形ABCD绕点A旋转一个角度得到AB₁C₁D₁ ，使得点D₁恰好落在BC边上，若AD＝2AB＝4，则CD₁的长为（）

A. 1 B. 2 C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 把 $\text{[math]}$ 米长的梯子斜靠在墙上，若梯子底端离墙 $\text{[math]}$ 米，则梯子顶端到离地面（）

A. $\text{[math]}$ 米 B. $\text{[math]}$ 米 C. $\text{[math]}$ 米 D. $\text{[math]}$ 米

单选题容易