1.
在等腰 中,
中, 是射线
是射线 上的动点,过点
上的动点,过点 作
作 (
( 始终在
始终在 上方),且
上方),且 , 连接
, 连接 .
.

(1)
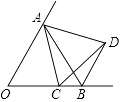
如图1,当点D在线段 上时,判断
上时,判断 的形状,并说明理由.
(2)
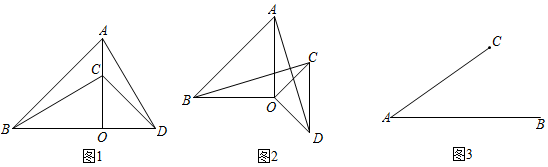
如图2,若D , E为线段
的形状,并说明理由.
(2)
如图2,若D , E为线段 上的两个动点,且
上的两个动点,且 , 连接
, 连接 , 求
, 求 的长.
(3)
如图3,若M为
的长.
(3)
如图3,若M为 中点,连接
中点,连接 , 在点
, 在点 的运动过程中,当
的运动过程中,当 时,
时, 的长最小,最小值是.
的长最小,最小值是.
【考点】
三角形-动点问题;