1.
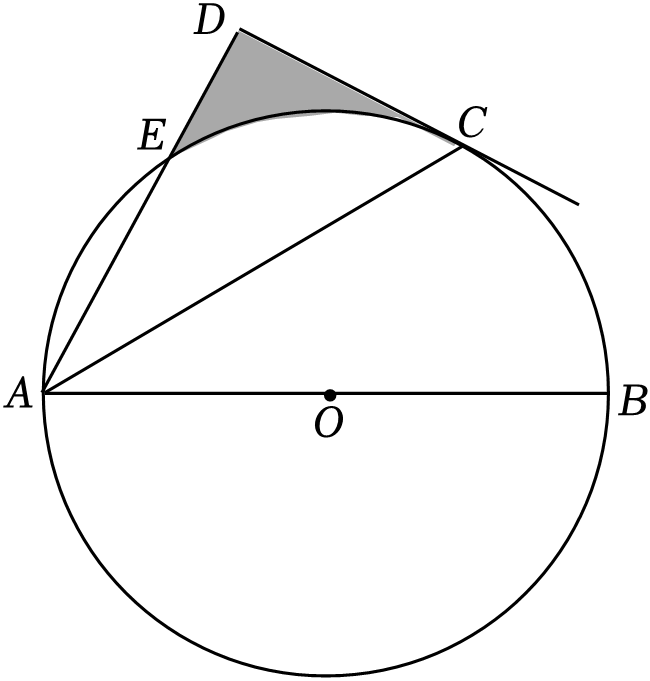
如图,⊙O是 的外接圆,
的外接圆, 是⊙O的直径,
是⊙O的直径, .
.

(1)
求证: 是⊙O的切线;
(2)
若
是⊙O的切线;
(2)
若 于点
于点 ,
,  交
交 于点
于点 , 且
, 且 ,
,  , 求
, 求 的长.
的长.
【考点】
圆的综合题;