如图，要在街道l上修建一个牛奶售卖点D．（街道用直线l表示）

1. 如图，要在街道l上修建一个牛奶售卖点D．（街道用直线l表示）

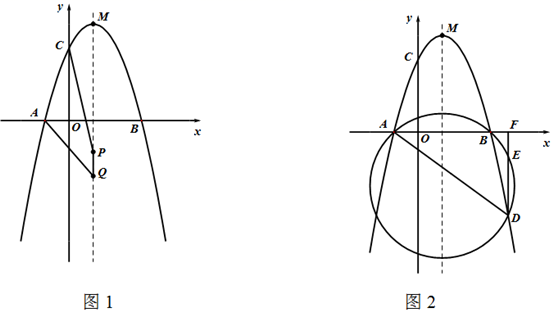
(1) 如图①，若牛奶售卖点D向小区A，B提供牛奶，则牛奶售卖点D应建在什么地方，才能使它到小区A ，B的距离之和最短？

(2) 如图②，若牛奶售卖点D向小区A，C提供牛奶，则牛奶售卖点D应建在什么地方，才能使它到小区A，C的距离之和最短？

【考点】

轴对称的应用-最短距离问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题困难

作图题普通

作图题普通

(2) 如图 $\text{[math]}$ ，在 $\text{[math]}$ 内部有两点 $\text{[math]}$ 、 $\text{[math]}$ ，是否在 $\text{[math]}$ 、 $\text{[math]}$ 上分别存在点 $\text{[math]}$ 、 $\text{[math]}$ ，使彻 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，四点组成的四边形的周长最短，找出 $\text{[math]}$ 、 $\text{[math]}$ 两点，保留作图痕迹．

作图题普通

x	…	$\text{[math]}$	0	1	2	3	…
y	…	0	3	4	3	0	…