1.
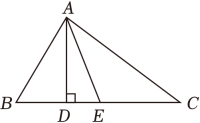
如图1,在△ABC中,AB=AC,P为底边BC上一点,PE⊥AB,PF⊥AC,CH⊥AB,垂足分别为E,F,H.易证PE+PF=CH.
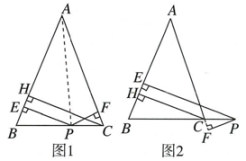
证明过程如下:
如图1,连结AP.
∵PE⊥AB,PF⊥AC,CH⊥AB,
∴S△ABP=AB·PE,S△ACP=
AC·PF,S△ABC=
AB·CH.
又∵S△ABP+S△ACP=S△ABC ,
∴AB·PE+AC·PF=AB·CH.
∵AB=AC,
∴PE+PF=CH.
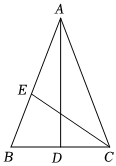
如图2,当P为BC延长线上的点时,其他条件不变,PE,PF,CH又有怎样的数量关系?请写出你的猜想,并加以证明.
【考点】
三角形的面积;
等腰三角形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练