1.
某学习小组在探究三角形全等时,发现了下面这种典型的基本图形,如下图

(1)
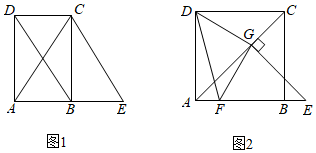
已知:在 中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E . 则线段DE与BD、CE的数量关系为.
(2)
组员小刘想,如果三个角不是直角,那(1)中的结论是否会成立呢?如图2,将(1)中的条件改为:在
中,∠BAC=90°,AB=AC , 直线l经过点A , BD⊥直线l , CE⊥直线l , 垂足分别为点D、E . 则线段DE与BD、CE的数量关系为.
(2)
组员小刘想,如果三个角不是直角,那(1)中的结论是否会成立呢?如图2,将(1)中的条件改为:在 中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=
中,AB=AC , D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC= , 其中
, 其中 为任意锐角或钝角.如果(1)中的结论成立,请证明;如不成立,请说明理由.
(3)
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过
为任意锐角或钝角.如果(1)中的结论成立,请证明;如不成立,请说明理由.
(3)
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过 的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.
的边AB、AC向外作正方形ABDE和正方形ACFG , AH是BC边上的高,延长HA交EG于点I , 求证:I是EG的中点.
【考点】
三角形全等及其性质;
三角形全等的判定;
能力提升
真题演练