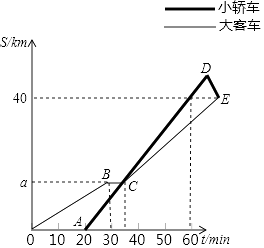
在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．小明和小亮相约到公园游玩已知小明家，小亮家到公园的距离相同，小明先骑车到达超市，购买了一些食物和饮用水，然后再骑车到达公园，小明出发后，小亮骑车从家出发直接到达公园，给出的图象中单位：反映了这个过程中小明骑行的路程，请根据相关信息，解答下列问题：

0 返回首页

1. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
小明和小亮相约到公园游玩 $\text{[math]}$ 已知小明家，小亮家到公园的距离相同，小明先骑车 $\text{[math]}$ 到达超市，购买了一些食物和饮用水，然后再骑车 $\text{[math]}$ 到达公园，小明出发 $\text{[math]}$ 后，小亮骑车从家出发直接到达公园，给出的图象中 $\text{[math]}$ 单位： $\text{[math]}$ 反映了这个过程中小明骑行的路程，请根据相关信息，解答下列问题：

(1) 填表：

小明离开家的时间 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
小明骑行的路程 $\text{[math]}$		$\text{[math]}$

(2) 填空：
$\text{[math]}$ 小明购物的超市到公园的距离是 $\text{[math]}$ ；
$\text{[math]}$ 小亮骑车的速度为 $\text{[math]}$ ；
$\text{[math]}$ 在小明和小亮从各自的家到公园的途中，当两人到公园的距离相同时，小明离开家的时间为 $\text{[math]}$ ；
$\text{[math]}$ 当小亮到达公园时，小明距公园还有 $\text{[math]}$