已知，，，，垂足分别为点D ， E ．

1. 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点D ， E ．

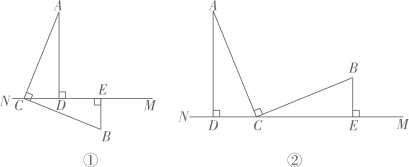
(1) 如图①，求证： $\text{[math]}$

(2) 如图②，（1）中的结论还成立吗？如果不成立，请写出线段AD ， BE ， DE之间的数量关系，并说明理由．

【考点】

三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 某建筑测量队为了测量一栋居民楼ED的高度，在大树AB与居民楼ED之间的地面上选了一点C，使B，C，D在一直线上，测得大树顶端A的视线AC与居民楼顶端E的视线EC的夹角为90°，若AB=CD=12米，BD=64米，请计算出该居民楼ED的高度.

解答题普通

2. 学习《利用三角形全等测距离》后，“开拓”小组同学就“测量河两岸 $\text{[math]}$ 、 $\text{[math]}$ 两点间距离”这一问题，设计了如下方案：如图，在点 $\text{[math]}$ 所在河岸同侧平地上取点 $\text{[math]}$ 和点 $\text{[math]}$ ．使点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在一条直线上，且 $\text{[math]}$ ，测得 $\text{[math]}$ ， $\text{[math]}$ ，在 $\text{[math]}$ 的延长线上取一点 $\text{[math]}$ ，使 $\text{[math]}$ ，这时测得 $\text{[math]}$ 的长就是 $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离．你同意他们的说法吗？请说明理由．

解答题普通

3. 如图，已知点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ．猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系并证明．

解答题普通