1.
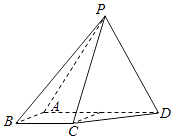
如图,四棱锥 的底面ABCD是菱形,
的底面ABCD是菱形, ,
,  ,
,  , E为PD的中点.
, E为PD的中点.

(1)
求证: 平面ACE;
(2)
求三棱锥
平面ACE;
(2)
求三棱锥 的体积.
的体积.
【考点】
棱柱、棱锥、棱台的体积;
直线与平面平行的判定;