1.


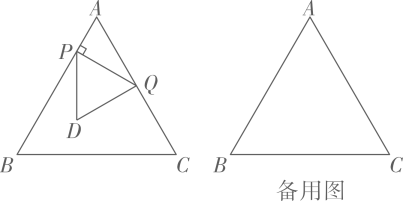
【探索发现】如图1,等腰直角三角形中,
,
, 直线
经过点
, 过
作
于点
. 过
作
于点
, 则
, 我们称这种全等模型为“k型全等”.(不需要证明)
【迁移应用】已知:直线的图象与x轴、y轴分别交于A、B两点.
(1)
如图2,当 时,在第二象限构造等腰直角
时,在第二象限构造等腰直角 ,
,  ;
(2)
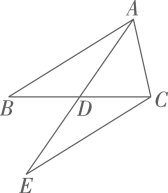
如图3,当k的取值变化,点A随之在x轴负半轴上运动时,在y轴左侧过点B作
;
(2)
如图3,当k的取值变化,点A随之在x轴负半轴上运动时,在y轴左侧过点B作 , 并且
, 并且 , 连接
, 连接 , 问
, 问 的面积是否发生变化?若不变,请求出这个定值.若变,请说明理由;
(3)
【拓展应用】如图4,在平面直角坐标系,点
的面积是否发生变化?若不变,请求出这个定值.若变,请说明理由;
(3)
【拓展应用】如图4,在平面直角坐标系,点 , 过点B作
, 过点B作 轴于点A,作
轴于点A,作 轴于点C,P为线段
轴于点C,P为线段 上的一个动点,点
上的一个动点,点 位于第一象限.问点A,P,Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出a的值;若不能,请说明理由.
位于第一象限.问点A,P,Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出a的值;若不能,请说明理由.
①直接写出 ,
;
②点C的坐标是;
【考点】
三角形的面积;
三角形全等及其性质;
真题演练