1.
如图,在平面直角坐标系中,抛物线 经过点
经过点 . 点
. 点 ,
,  在此抛物线上,其横坐标分别为
在此抛物线上,其横坐标分别为 , 连接
, 连接 ,
,  .
.
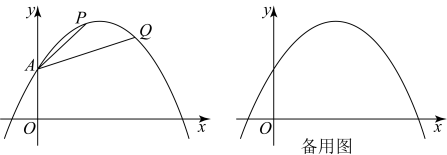
(1)
求此抛物线的解析式.
(2)
当点 与此抛物线的顶点重合时,求
与此抛物线的顶点重合时,求 的值.
(3)
当
的值.
(3)
当 的边与
的边与 轴平行时,求点
轴平行时,求点 与点
与点 的纵坐标的差.
(4)
设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为
的纵坐标的差.
(4)
设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为 , 在点
, 在点 与点
与点 之间部分(包括点
之间部分(包括点 和点
和点 )的最高点与最低点的纵坐标的差为
)的最高点与最低点的纵坐标的差为 . 当
. 当 时,直接写出
时,直接写出 的值.
的值.
【考点】
二次函数的最值;
二次函数y=ax²+bx+c的图象;
二次函数y=ax²+bx+c的性质;

