1.
综合与实践
【问题情境】数学活动课上,老师给出了这样一个问题:
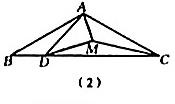
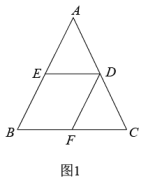
如图1,在中,
, 射线AD平分
, 将射线AD绕点
逆时针旋转
, 得到射线
, 在射线
上取点
, 使得
, 连接BE分别交AD,AC于点M,N,连接CE.问:
之间的数量关系是什么?线段DM,CN之间的数量关系是什么?

【特例探究】“勤奋”小组的同学们先将问题特殊化,探究过程如下:
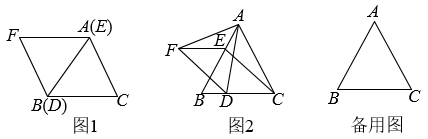
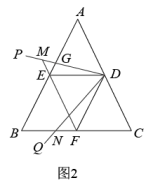
甲同学:当时,如图2,通过探究可以发现,
都是等腰三角形;
乙同学:可以证明 , 得到
;
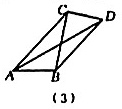
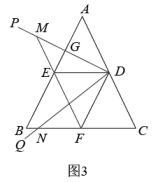
丙同学:过点做
, 垂足为
, 如图3,则
;
丁同学:可以证明 , 则
, …
(1)
根据以上探究过程,得出结论:
(2)
【类比探究】
(3)
【迁移应用】
①之间的数量关系是;
②线段DM,CN之间的数量关系是.
“智慧”小组的同学们在“勤奋”小组的基础上,进一步探究一般情形,当时,如图1,⑴中的两个结论是否仍然成立?如果成立,请仅就图1的情形进行证明;如果不成立,请说明理由。
“创新”小组的同学们改变了条件,当时,如图4,若射线AD是
的三等分角线,
, 其他条件不变,请直接写出MN的长.

【考点】
三角形的综合;
能力提升
真题演练