1.
综合与实践
问题情境:
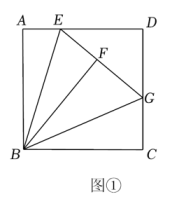
如图①,点E为正方形内一点,
, 将
绕点B按顺时针方向旋转
, 得到
(点A的对应点为点C).延长
交
于点F,连接
.

(1)
猜想证明:
(2)
如图②,若 , 请猜想线段
, 请猜想线段 与
与 的数量关系并加以证明;
(3)
解决问题:
的数量关系并加以证明;
(3)
解决问题:
试判断四边形的形状,并说明理由;
如图①,若 , 请直接写出
的长.
【考点】
正方形的性质;
四边形的综合;
能力提升
真题演练