1.
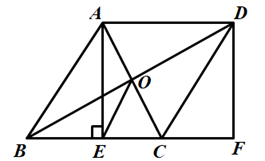
已知 是菱形
是菱形 的对角线,
的对角线, , 点E是直线
, 点E是直线 上的一个动点,连接
上的一个动点,连接 , 以
, 以 为边作菱形
为边作菱形 , 并且使
, 并且使 , 连接
, 连接 , 当点E在线段
, 当点E在线段 上时,如图
上时,如图 , 易证:
, 易证: .
.
(1)
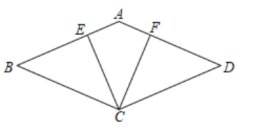
当点E在线段 的延长线上时(如图
的延长线上时(如图 ),猜想
),猜想 ,
,  ,
,  之间的关系并证明;
(2)
当点E在线段
之间的关系并证明;
(2)
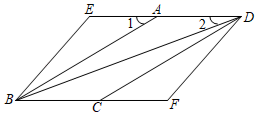
当点E在线段 的延长线上时(如图
的延长线上时(如图 ),直接写出
),直接写出 ,
,  ,
,  之间的关系.
之间的关系.
【考点】
菱形的性质;
三角形全等的判定-SAS;
能力提升
真题演练