1.
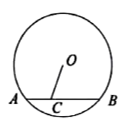
《九章算术》标志中国古代数学形成了完整的体系,第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表述为:“如图, 是
是 的直径,弦
的直径,弦 于点
于点 ,
,  寸,
寸, 寸,求直径
寸,求直径 的长,”请你解答这个问题.
的长,”请你解答这个问题.

【考点】
垂径定理的实际应用;
能力提升
变式训练
拓展培优
真题演练