1.
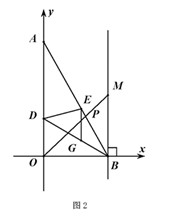
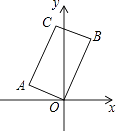
如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
坐标与图形性质;
全等三角形的判定与性质;