1.
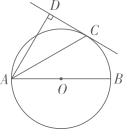
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且CF是⊙O的切线．
(1)
求证：∠DCF＝∠CAD．
(2)
探究线段CF，FD，FA的数量关系并说明理由；
(3)
若cosB＝
， AD＝2，求FD的长．
【考点】
切线的性质;
相似三角形的判定与性质;
