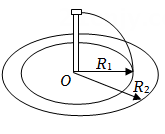
1.
如图所示,细绳一端系着质量为M=0.5kg的物体,静止在水平面上,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N。现使此平面绕中心轴线转动,求:角速度ω在什么范围内m处于静止状态?(g=10m/s2)

【考点】
匀速圆周运动;