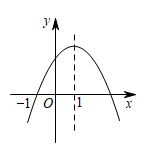1.
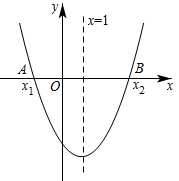
已知:二次函数
(1)
m为何值时,此抛物线必与x轴相交于两个不同的点;
(2)
m为何值时,这两个交点在原点的左右两边;
(3)
m为何值时,此抛物线的对称轴是y轴;
(4)
m为何值时,这个二次函数有最大值 .
.
【考点】
二次函数的最值;
二次函数图象与坐标轴的交点问题;