1.
如图

(1)
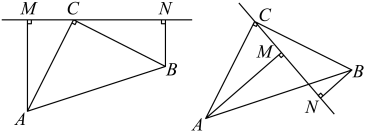
证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.如图1,已知: 平分
平分 , 点
, 点 在
在 上,
上, ,
,  , 垂足分别为
, 垂足分别为 ,
,  . 求证:
. 求证: .
(2)
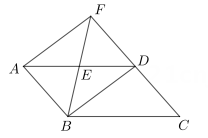
如图2,在
.
(2)
如图2,在 中,
中, 平分
平分 , 交
, 交 于点
于点 ,
,  于点
于点 ,
,  于点
于点 ,
,  , 若
, 若 , 求
, 求 的长.
的长.
【考点】
三角形的面积;
三角形全等的判定-AAS;