1.
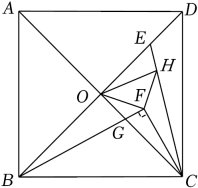
如图,正方形ABCD的对角线相交于点O.点E是线段DO上一点,连接CE.点F是∠OCE的平分线上一点,且BF⊥CF与CO相交于点G.点H是线段CE上一点,且CO=CH.
(1)
若OF=5,求FH的长;
(2)
求证:BF=OH+CF.
【考点】
平行四边形的判定;
正方形的性质;
三角形全等的判定-SAS;
角平分线的概念;


