1.
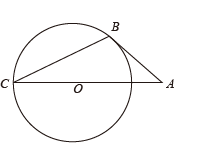
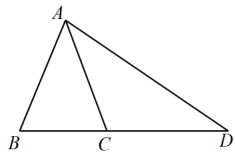
在证明圆周角定理时,某学习小组讨论出圆心与圆周角有三种不同的位置关系(如图1,2,3所示),小敏说:当圆心O在∠ACB的边上时,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.小亮说:当圆心O在∠ACB的内部或外部时,可以通过添加直径这条辅助线,把问题转化为圆心O在∠ACB的边上时的特殊情形来解决.请选择图2或图3中的一种,完成证明.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.已知:如图,在 求证: | ||
|
|
|
【考点】
三角形的外角性质;
等腰三角形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练